Page 399 - OLİMPİK SONLU MATEMATİK

ÝÇERME DIÞARMA (DAHÝLÝYET HARÝCÝYET) PRENSÝBÝ ALIÞTIRMALAR VE ÇÖZÜMLERÝ 6.1

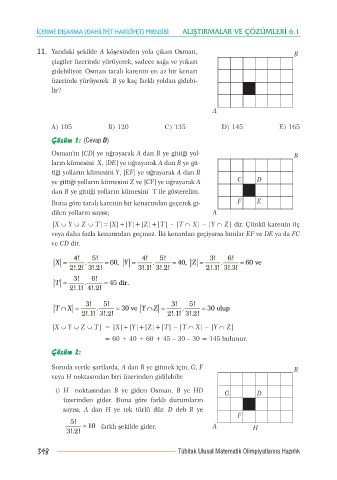
11. Yan da ki þe kil de A kö þe sin den yo la çý kan Os man,
çiz gi ler üze rin de yü rü ye rek, sa de ce sa ða ve yu ka rý
gi de bi li yor. Os man ta ra lý ka re nin en az bir ke na rý
üze rin de yü rü ye rek B ye kaç fark lý yol dan gi de bi -
lir?

A) 105 B) 120 C) 135 D) 145 E) 165
Çö züm 1:
Çö züm 1: (Ce vap D)
Os man'ýn [CD] ye uð ra ya rak A dan B ye git ti ði yol -
la rýn kü me si ni X, [DE] ye uð ra ya rak A dan B ye git -
ti ði yol la rýn kü me si ni Y, [EF] ye uð ra ya rak A dan B
ye git ti ði yol la rýn kü me si ni Z ve [CF] ye uð ra ya rak A
dan B ye git ti ði yol la rýn kü me si ni T ile gös te re lim.

Bu na gö re ta ra lý ka re nin bir ke na rýn dan ge çe rek gi -
di len yol la rýn sa yý sý;
|X Y Z T|=|X|+|Y|+|Z|+|T| – |T X| – |Y Z| dir. Çünkü karenin üç
veya daha fazla kenarýndan geçmez. Ýki kenardan geçiyorsa bunlar EF ve DE ya da FC
ve CD dir.

|X Y Z T|= |X|+|Y|+|Z|+|T| – |T X| – |Y Z|
= 60 + 40 + 60 + 45 – 30 – 30 = 145 bulunur.
Çö züm 2:
Çö züm 2:
Soruda verile þartlarda, A dan B ye gitmek için, G, F
veya H noktasýndan biri üzerinden gidilebilir.
i) H noktasýndan B ye giden Osman, B ye HD
üzerinden gider. Buna göre farklý durumlarýn
sayýsý; A dan H ye tek türlü dür. D deb B ye

farklý þekilde gider.

398 Tübitak Ulusal Matematik Olimpiyatlarýna Hazýrlýk