Page 398 - OLİMPİK SONLU MATEMATİK

ALIÞTIRMALAR VE ÇÖZÜMLERÝ 6.1 ÝÇERME DIÞARMA (DAHÝLÝYET HARÝCÝYET) PRENSÝBÝ

Diðer taraftan, C ve C kümesinin tümleyenini göstermek üzere,
4
4
s(A B) = 10 – s((A B) ) = 10 – 8 4
olur. Son iki eþitlik yerlerine yazýlýrsa,
4
4
4
4
s(A B) = 2(10 – 9 ) – (10 – 8 ) = 974
bulunur.

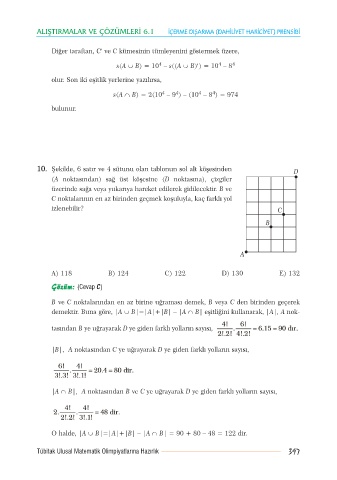
10. Þekilde, 6 satýr ve 4 sütunu olan tablonun sol alt köþesinden
(A noktasýndan) sað üst köþesine (D noktasýna), çizgiler
üzerinde saða veya yukarýya hareket edilerek gidilecektir. B ve
C noktalarýnýn en az birinden geçmek koþuluyla, kaç farklý yol
izlenebilir?

A) 118 B) 124 C) 122 D) 130 E) 132
Çö züm:
Çö züm: (Ce vap C)
B ve C noktalarýndan en az birine uðramasý demek, B veya C den birinden geçerek
demektir. Buna göre, |A B|=|A|+|B| – |A B| eþitliðini kullanarak, |A|, A nok-

tasýndan B ye uðrayarak D ye giden farklý yollarýn sayýsý,

|B|, A noktasýndan C ye uðrayarak D ye giden farklý yollarýn sayýsý,

|A B|, A noktasýndan B ve C ye uðrayarak D ye giden farklý yollarýn sayýsý,

O halde, |A B|=|A|+|B| – |A B| = 90 + 80 – 48 = 122 dir.

Tübitak Ulusal Matematik Olimpiyatlarýna Hazýrlýk 397