Page 352 - OLİMPİK SONLU MATEMATİK

ALIÞTIRMALAR VE ÇÖZÜMLERÝ 4.1 OLASILIK

Çö züm:
Çö züm: (Ce vap C)
Yarýçapý 1 birim ve merkezi O(0, 0) yani birim çember üzerinde A, B, C gibi üç nokta
alalým. T(1, 0) noktasýndan A, B ve C noktalarýna olan yaylarýn uzunluðu sýrasýyla a, b

ve c olsun. Gerektiðinde döndürme yapýlabilir. olarak alabiliriz. Buna göre, b ve

c uzunluklarý [0, 2] aralýðýndan rastgele seçilebilir. (b, c) sýralý ikilisini bc- düzleminde-
ki kenar uzunluðu 2 olan bir kareden seçelim. Aþaðýdaki eþitsizlikler gerçekleþirse,
sorudaki þartlarda saðlanmýþ olur.

Son eþitsizlik için saðlanýr.

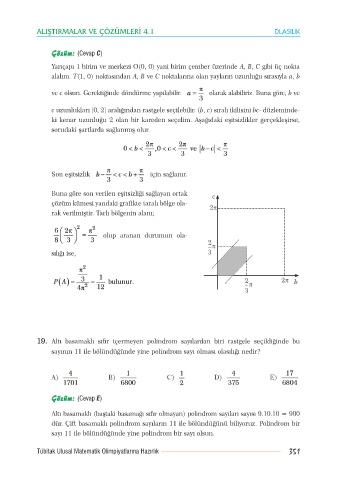
Bu na gö re son ve ri len eþit siz li ði sað la yan or tak
çö züm kü me si yan da ki gra fik te ta ra lý böl ge ola -

rak ve ril miþ tir. Tar lý böl ge nin ala ný;

olup ara nan du ru mun ola -

sýlığı ise,

19. Altý basamaklý sýfýr içermeyen polindrom sayýlardan biri rastgele seçildiðinde bu
sayýnýn 11 ile bölündüðünde yine polindrom sayý olmasý olasýlýðý nedir?

A) B) C) D) E)

Çö züm:
Çö züm: (Ce vap E)
Altý basamaklý (baþtaki basamaðý sýfýr olmayan) polindrom sayýlarý sayýsý 9.10.10 = 900
dür. Çift basamaklý polindrom sayýlarýn 11 ile bölündüðünü biliyoruz. Polindrom bir
sayý 11 ile bölündüðünde yine polindrom bir sayý olsun.

Tübitak Ulusal Matematik Olimpiyatlarýna Hazýrlýk 351